行測(cè)數(shù)量關(guān)系工程問題中的基本公式大家已經(jīng)非常熟悉:工作總量=工作效率×工作時(shí)間。而在實(shí)際考試當(dāng)中,工程問題多數(shù)情況會(huì)考查多者合作,就稍顯復(fù)雜了,那多者合作問題該如何解題呢?須知世異則事異,事異則備變,今天華公教育帶大家一起來了解如何利用特值法讓多者合作問題變簡(jiǎn)單!
多者合作研究的是多個(gè)主體通過一定方式合作完成工作的問題,合作效率等于各個(gè)主體的效率加和。解決多者合作問題,可適當(dāng)結(jié)合題干信息將未知量設(shè)為特值,來簡(jiǎn)化運(yùn)算。
一、已知多個(gè)主體完工時(shí)間,可設(shè)工作總量為1或完工時(shí)間的最小公倍數(shù)為特殊值
例1
某水池裝有甲、乙、丙三根注水管,單獨(dú)開甲管10分鐘可將水注滿,單獨(dú)開乙管15分鐘可將水注滿,單獨(dú)開丙管6分鐘可將水注滿,那么三管齊開需要多少分鐘可以將水注滿?
A.5 B.4 C.3 D.2
【華公解析】C。所求為三管齊開的時(shí)間,根據(jù)工程問題基本公式,需要用工作總量除以三個(gè)管的效率加和。題干給出了甲乙丙各自將水注滿的時(shí)間,因此可設(shè)工作總量為特值。
方法一:設(shè)工作總量為1,甲的效率即為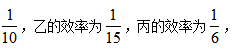 所求時(shí)間為
所求時(shí)間為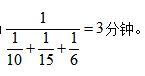 故選C項(xiàng)。
故選C項(xiàng)。

方法二中三人的效率可直接表示為整數(shù),明顯計(jì)算更加簡(jiǎn)單,因此可以考慮直接設(shè)工作總量為時(shí)間的最小公倍數(shù),以簡(jiǎn)化運(yùn)算過程。
二、已知多個(gè)主體效率的比例關(guān)系時(shí),一般根據(jù)效率關(guān)系將效率最簡(jiǎn)比設(shè)為特值
例2
甲、乙、丙三隊(duì)合作修馬路,已知甲隊(duì)每天修的路程是丙隊(duì)的3倍,乙隊(duì)每天修的路程是丙隊(duì)的2倍,三隊(duì)合作6天完成總路程的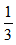 后,甲休息6天后接著干,乙休息9天后接著干,丙不休息一直干,最終完工。則開始到完工需要多少天?
后,甲休息6天后接著干,乙休息9天后接著干,丙不休息一直干,最終完工。則開始到完工需要多少天?
A.24 B.28 C.32 D.36
【華公解析】A。根據(jù)題意可知“甲的效率是丙的3倍,乙的效率是丙的2倍”,可知甲、乙、丙三者效率的比例關(guān)系為3:2:1,設(shè)丙的效率為1,則乙的效率為2,甲的效率為3;三隊(duì)6天完成總路程的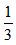 ,則剩余部分按原效率需12天完成,剩余工作量為(3+2+1)×12,設(shè)剩余工作還需時(shí)間為t,根據(jù)甲乙丙三人的工作量加和等于剩余工作量,可列方程3×(t-6)+2×(t-9)+1×t=(3+2+1)×12,解得t=18,共用時(shí)間6+18=24天。故選A項(xiàng)。
,則剩余部分按原效率需12天完成,剩余工作量為(3+2+1)×12,設(shè)剩余工作還需時(shí)間為t,根據(jù)甲乙丙三人的工作量加和等于剩余工作量,可列方程3×(t-6)+2×(t-9)+1×t=(3+2+1)×12,解得t=18,共用時(shí)間6+18=24天。故選A項(xiàng)。
通過華公教育上述兩個(gè)例子可以發(fā)現(xiàn),使用特值法解決多者合作問題可以簡(jiǎn)化運(yùn)算,一般可再結(jié)合工作總量列方程求解。百尺竿頭須進(jìn)步,希望同學(xué)們不要疏于練習(xí),博觀而約取,厚積而薄發(fā)!


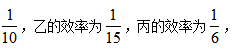 所求時(shí)間為
所求時(shí)間為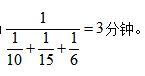 故選C項(xiàng)。
故選C項(xiàng)。

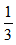 后,甲休息6天后接著干,乙休息9天后接著干,丙不休息一直干,最終完工。則開始到完工需要多少天?
后,甲休息6天后接著干,乙休息9天后接著干,丙不休息一直干,最終完工。則開始到完工需要多少天?
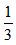 ,則剩余部分按原效率需12天完成,剩余工作量為(3+2+1)×12,設(shè)剩余工作還需時(shí)間為t,根據(jù)甲乙丙三人的工作量加和等于剩余工作量,可列方程3×(t-6)+2×(t-9)+1×t=(3+2+1)×12,解得t=18,共用時(shí)間6+18=24天。故選A項(xiàng)。
,則剩余部分按原效率需12天完成,剩余工作量為(3+2+1)×12,設(shè)剩余工作還需時(shí)間為t,根據(jù)甲乙丙三人的工作量加和等于剩余工作量,可列方程3×(t-6)+2×(t-9)+1×t=(3+2+1)×12,解得t=18,共用時(shí)間6+18=24天。故選A項(xiàng)。




