縱觀各大系統考試真題，不定方程都考的都比較簡單，且變型少，技巧性比較強，當掌握其解題方法后，不定方程只要考到就是送分，重要的話說三遍，不定方程考到就是送分，考到就是送分，送分……

常見考察形式為：

①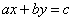（其中）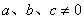

②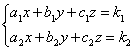（不定方程組）

解不定方程的方法：代入排除法，具體如下：

①直接代入法：直接要求的是或者

例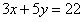：,其中x、y都是正整數，求y=（   ）。

A.2      B.3     C.4       D.5

【答案】A

【解析】要求的是y的值，A、B、C、D中一定有一個是正確答案，所以只需要一個個帶入驗證即可，只需要保證求出來的x也是正整數就可以，帶入A選項，當y=2時，x=4，滿足條件，繼續驗證后面的選項都不滿足，所以A當選。

②奇偶性：當x、y的系數為一奇一偶時，可以使用奇偶性解不定方程。

例: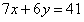,其中x、y都是正整數，求x=（   ）。

A.3      B.4     C.5       D.6

【答案】C

【解析】6y為偶數，41為奇數，由奇偶性運算可得7x為奇數，則x也是奇數，故可以排除B、D選項，剩下A、C，帶入A選項，當x=3時，21+6y=41，此時y不是整數，排除，答案選C。

③倍數特性：當x、y的系數與右邊常數存在倍數關系時，可以使用倍數特性解不定方程。

例: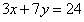，其中x、y都是正整數，求x=（   ）。

A.1      B.2     C.3       D.4

【答案】A

【解析】3x和24都是3的倍數，所以7y也是3的倍數，又y是整數，所以y是3的倍數，滿足3的倍數有3、6、9……，但必須得保證x是正整數，所以只有當y=3時，x=1，符合條件，答案選A。

④尾數法：當x或y的系數為5的倍數時，可以使用尾數法解不定方程(一般會結合奇偶性)。

例: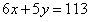，其中x、y都是正整數，求x-y=(    )。

A.3      B.4     C.5       D.6

【答案】D

【解析】其中6x和113分別是偶數和奇數，所以5y這個整體也是奇數，兩個數的乘積是奇數，進一步得到y也是奇數，一個奇數與5相乘，它的尾數為5，所以6x的尾數為8,6與3或8相乘的尾數為8,故得到x的尾數為3或8，滿足x的數有3、8、13、18……，當x=3時，y=19，x＜y，不符；當x=8時，y=13，同理不符；當x=13時，y=7，此時x-y=6，故答案選D。

⑤賦值法：大多數情況為不定方程組中含有3個未知數x、y、z，且求的是含有“x+y+z”的整體時，一般的操作為令x、y、z中的一項為0。

例:已知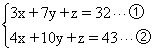，求x+y+z=(    )。

A.12 B.11 C.10 D.9

【答案】C

【解析】令y=0,則相當于將y消去了，則方程變為了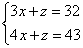，兩式相減解得x=11,z=-1,根據題意可知要求的是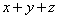的值，故。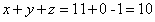

賦值法的特征為不會影響結果，也可以令x或z為0,最終“x+y+z”的結果始終不變，當然這里最簡單的處理方式就是令y=0,后續的計算比較簡單。

一般地像這一類型的題，還可以采取用配系數法，即令①×3-②×2結果剛好等于x+y+z=32×3-43×2=10，但這一方法要求對數字明感性比較強。